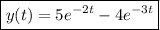Question

1a. Solve the differential equations

y" + 5y' + 6y = 0, y(0) = 1 and y'(0) = 2

Note that each equation has right hand side zero. So, you don’t have to use the Laplace transform. You just use the characteristic equaiton.​

Answer 1

y'' + 5y' + 6y = 0

has characteristic equation

r² + 5r + 6 = (r + 2) (r + 3) = 0

with roots at r = -2 and r = -3, hence the differential equation's characteristic solution is

`y(t) = C_1 e^(-2t) + C_2 e^(-3t)`

Given that y(0) = 1 and y'(0) = 2, we have

`y(t) = C_1 e^(-2t) + C_2 e^(-3t) \implies 1 = C_1 + C_2`

`y'(t) = -2C_1 e^(-2t) - 3C_2 e^(-3t) \implies 2 = -2C_1 - 3C_2`

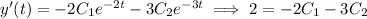
and solving the resulting system of equations yields C₁ = 5 and C₂ = -4.

So the particular solution to the ODE is

`\boxed{y(t) = 5 e^(-2t) - 4 e^(-3t)}`