Question

Help.meee.........................​

Answer 1

...

Step-by-step explanation:

.................

Answer 2

Solution given:

t=
`2π \sqrt{(m)/(g)}`

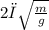
where

t=time and it's dimension is [T¹]

m=mass and its dimension is [M¹]

dimension of constant term is nothing.

t=
`2π \sqrt{(m)/(g)}`

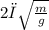
squaring on both side

we get

t²=4π²*
`(m)/(k)`

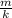
since 4π² has no dimension

Dimension of t²=[T²]

Dimension of m=[M¹]

Dimension of k=?

By using

The principle of homogeneity of dimension we get

Dimension of t²=dimension of
`(m)/(k)`

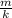
[T²]=
`([M¹])/(K)`

doing crisscrossed multiplication

K=
`([M¹])/([T²])`

dimension of k is
`[M¹T^(-2)]`or
`[M¹L^0T^(-2)]`

since length is absent