Question

Please solve with explanation

Answer 1

Explanation:

Since the ball is going upwards, then down, we have a parabola.

In the form of

`- {x}^(2) + bx + c = 0`

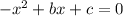
The leading coeffeicent is negative because we are increasing then decreasing.

Let use t for seconds and h is height.

So we have a function

`h(t) = - {t}^(2) + b(t) + c`

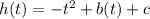
Since I'm have no information: I'm use calculus and physics to solve this.

All objects fall at the speed of

`- 9.8 \frac{m}{ {s}^(2) }`

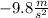
Which is the unit for acclereation.

Since we have are trying to a poisition versus time function, note that the anti derivative of acclereation will give us velocity. So let calculate that

`(d)/(dx) (a) = - 9.8x`

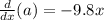
Then note that the anti derivative of velocity is poistion.

`(d)/(dx) (v) = - 4.9 {x}^(2)`

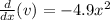
So we know our leading coeffeicent, is -4.9x^2.

The ball is initially launched at a speed of 15 m/s. So the first derivative of the function at x=0, should be 15.

`(d)/(dx) (x) = - 4.9 {x}^(2) + bx`

`v = - 9.8x + b`

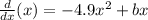
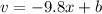
Since 0 times anything is 0, b must be 15 in order to have a first derivative of 15.

Since 0,1 is the y intercept, c will be 1.

So our answer is

`- 4.9 {x}^(2) + 15x + 1 = 0`

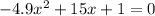
b). When x=1, we get a height of 11.1. Plug in 1 into the function, and we get 11.1

c). Set the function equal to zero and use quadratic formula to solve. You will get 3.13 seconds.

d. The max occurs when the velocity is 0. So we can first differentiate the function, which we will get

`- 9.8x + 15 = 0`

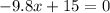
Then we solve for x.

We get 1.5 seconds. Then plug in 1.5 into the function, we get 12.5. So the max height is 12.5 and this occurs at 1.5 seconds.

e).