6 is of course a multiple of 6, so you need only focus on
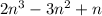 .
.
When n = 1, this expression has a value of 2 - 3 + 1 = 0, which is indeed a multiple of 6 (and any natural number for that matter).
Assume that 6 divides
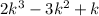 .
.
Now,
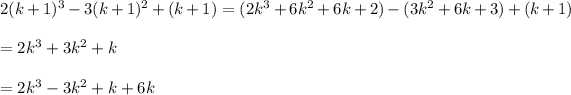
and this is divisible by 6. (6k is obviously a multiple of 6; that 6 divides the other three terms is due to the induction hypothesis.)