Question

Please answer this question​

Answer 1

We have the given indefinite integral ;

`{:\implies \quad \displaystyle \sf \int (x+1)/(x(xe^(x)+2))dx}`

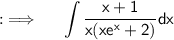
We will use substitution hence to solving this integral

Now , put ;

`{:\implies \quad \sf e^(x)=u}`

So that :

`{:\implies \quad \sf dx=(du)/(u)\quad and\quad log(u)=x}`

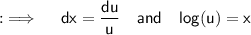
Now , putting the values in the integral , it can be written as ;

`{:\implies \quad \displaystyle \sf \int \frac{log(u)+1}{log(u)\{ulog(u)+2\}}* (du)/(u)}`

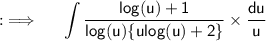
Now , we will again use substitution method for making the integral easy. So put ;

`{:\implies \quad \displaystyle \sf ulog(u)+2=v}`

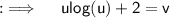
So that ;

`{:\implies \quad \displaystyle \sf du=(dv)/(log(u)+1)\quad and\quad ulog(u)=v-2}`

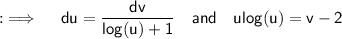
Now , we have ;

`{:\implies \quad \displaystyle \sf \int \frac{\cancel{\{log(u)+1\}}}{log(u)v}* \frac{dv}{\cancel{\{log(u)+1\}}u}}`

`{:\implies \quad \displaystyle \sf \int \frac{dv}{v\{ulog(u)\}}}`

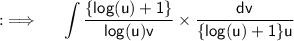
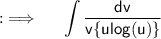
Now , putting the value of ulog(u) = v - 2

`{:\implies \quad \displaystyle \sf \int (dv)/(v(v-2))}`

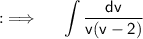
Now , using partial fraction decomposition , ths given integral can be further written as ;

`{:\implies \quad \displaystyle \sf (1)/(2)\int \left((1)/(v-2)-(1)/(v)\right)dv}`

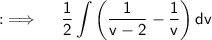
Now ,as integrals follow distributive property. So ;

`{:\implies \quad \displaystyle \sf (1)/(2)\left(\int (1)/(v-2)dv-\int (1)/(v)dv\right)}`

`v-2`

`(v-2)/(v)\bigg`

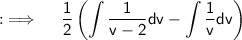
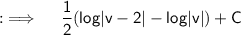
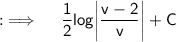
Putting value of v ;

`(ulog(u)+2-2)/(ulog(u)+2)\bigg`

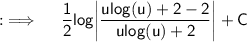
Now, putting value of u ;

`(e^(x)log(e^(x)))/(e^(x)log(e^(x))+2)\bigg`

`+C`

`{:\implies \quad \therefore \displaystyle \underline{\underline +C}}`

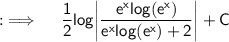
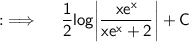
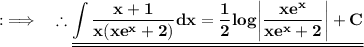
Used Concepts :-

• 
  `{\boxed\displaystyle \bf \int (1)/(x)dx=log}`

• 
  `{\boxed{\displaystyle \bf (d)/(dx)(u\cdot v)=v(du)/(dx)+u(dv)/(dx)}}`

• 
  `{\boxed{\displaystyle \bf log(a)-log(b)=log\left((a)/(b)\right)}}`

• 
  `{\boxed{\displaystyle \bf log(a^b)=blog(a)}}`

• 
  `{\boxed{\displaystyle \bf (d)/(dx)\{log(x)\}=(1)/(x)}}`

• 
  `{\boxed{\displaystyle \bf (d)/(dx)(e^x)=e^(x)}}`