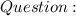Question

How can you simplify expressions containing negative exponents?

Answer 1

`Question:` ✧

How can you simplify expressions containing negative exponents? ✩

`ANSWER:` ✶

By reversing. ✳︎

`EXAMPLE:` ❄︎

`(1)/(2^(-2)) }` ✴︎

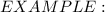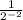The fraction is unhappy because of its negative exponent; it's so forlorn that it flops over: ❆ ▵ ❁

`} (2^(2) )/(1)` ✳︎ ✺

`(4)/(1)` ❅ ✸

`4`

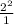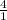Here's one more example: ☀︎

`23^(-2)` ☻ ⭐︎

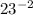OMG! The number is sobbing quietly. Let's rescue it!

How? ☺

Just by flopping it over ! ☆

Hope this helps! ✭

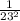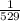`(1)/(23^(2) )` ♢ ★

`(1)/(529)` ☼

Answer 2

hope this short and sweet answer helps you

Explanation:

A negative exponent helps to show that a base is on the denominator side of the fraction line. In other words, the negative exponent rule tells us that a number with a negative exponent should be put to the denominator, and vice versa. For example, when you see x^-3, it actually stands for 1/x^3.