The parabola y = x ² and the line x + y = 12 intersect for
x ² = 12 - x
x ² + x - 12 = 0
(x - 3) (x + 4) = 0
===> x = 3
so you can compute the area by using two integrals,
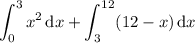
Then the area you want is
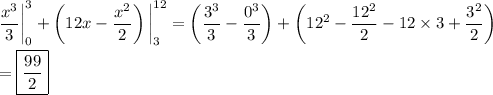
Alternatively, you can subtract the area bounded by y = x ², x + y = 12, and the y-axis in the first quadrant from the area of a triangle with height 12 (the y-intercept of the line) and length 12 (the x-intercept).
Such a triangle has area
1/2 × 12 × 12 = 72
and the area you want to cut away from this is given by a single integral,
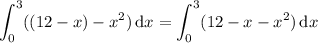
The integral has a value of
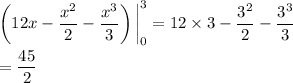
and so the area of the shaded region is again 72 - 45/2 = 99/2.