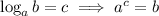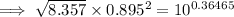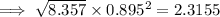Answer:
i) Using log law:
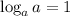
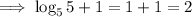
ii)
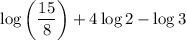
Using log law
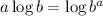 :
:
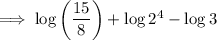
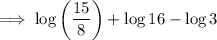
Using log law
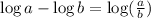 :
:
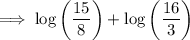
Using log law
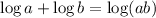 :
:
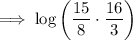
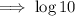
Using log law:
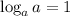
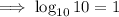
iii) Take log of base 10:
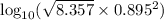
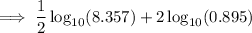
Log tables
The characteristic of the logarithm of a number is the exponent of 10 in its scientific notation.
The mantissa is found using the log tables and is always prefixed by a decimal point.
The row is the first two non-zero digits of the number, and the column is the 3rd digit of the number
Use the log tables to find
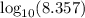 :
:
8.357 = 8.357 × 10⁰
⇒ characteristic = 0
log table: row 83, column 5 ⇒ mantissa 9217
(as there is a 4th digit) Mean difference 7 = 4
mantissa + mean difference = 9217 + 4 = 9221 ⇒ 0.9221
characteristic + mantissa = 0 + 0.9221 = 0.9221
Therefore,
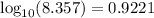
Use the log tables to find
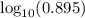 :
:
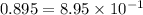
⇒ characteristic = -1
log table: row 89, column 5 ⇒ mantissa 9518⇒ 0.9518
characteristic + mantissa = -1 + 0.9518= -0.0482
Therefore,
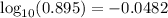
Therefore,
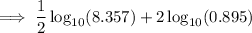
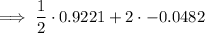
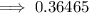
Therefore,
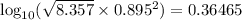
Using