Answer:
Ø
Explanation:
These equations are parallel, meaning they have SIMILAR rate of changes [slopes]. To prove it, convert the second equation from Standard Form to Slope-Intercept Form:
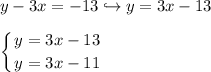
As you can see, both equations have a rate of change of 3, meaning we CANNOT obtain a solution here, therefore we have no solution.
I am joyous to assist you at any time.