Question

-3|9x-7|=2 Find the answer for x

Answer 1

Solving Equations with Absolute Expressions

Answer:

No Solutions

Explanation:

Given:

`-3|9x -7| = 2`

Rewriting the given equation:

`-3|9x -7| = 2 \\ |9x -7| = -(2)/(3)`

We have to realize that the right side of the equation,
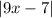`|9x -7|`, will always be positive no matter what real values of
`x` (because we're taking the absolute value of the expression) and we are equating it to a negative constant number,
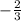`-(2)/(3)\\`. Something that is always positive will never be negative so there's no value for
`x` that satisfies the solution.

`\rule{6.5cm}{0.5pt}`

You may not read the following passage that I have written.

`\rule{6.5cm}{0.5pt}`

Solving by positive of the expression:

`9x -7 = -(2)/(3) \\ 9x = -(2)/(3) +7 \\ 9x = -(2)/(3) +(21)/(3) \\ 9x = (19)/(3) \\ 9x * (1)/(9) = (19)/(3) * (1)/(9) \\ x = (19)/(27)`

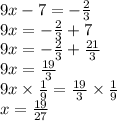
Solving by the negative of the expression:

`-(9x -7)= -(2)/(3) \\ 9x -7 = (2)/(3) \\ 9x = (2)/(3) +7 \\ 9x = (2)/(3) +(21)/(3) \\ 9x = (23)/(3) \\ 9x * (1)/(9) = (23)/(3) * (1)/(9) \\ x = (23)/(27)`

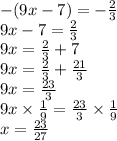
Checking:
`x = (19)/(27)\\`

`-3|9((19)/(27)) -7| \stackrel{?}{=} 2 \\ -3|(19)/(3) -7| \stackrel{?}{=} 2 \\ -3|(19)/(3) -(21)/(3)| \stackrel{?}{=} 2 \\ -3|-(2)/(3)| \stackrel{?}{=} \\ -3((2)/(3)) \stackrel{?}{=} 2 \\ -2 \stackrel{?}{=} 2 \\ -2 \\eq 2`

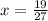
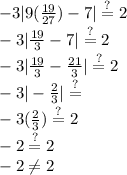
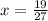`x = (19)/(27)\\` is an extraneous solution.

Checking:
`x = (23)/(27)\\`

`-3|9((23)/(27)) -7| \stackrel{?}{=} 2 \\ -3|(23)/(3) -7| \stackrel{?}{=} 2 \\ -3|(23)/(3) -(21)/(3)| \stackrel{?}{=} 2 \\ -3|(2)/(3)| \stackrel{?}{=} \\ -3((2)/(3)) \stackrel{?}{=} 2 \\ -2 \stackrel{?}{=} 2 \\ -2 \\eq 2`

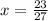
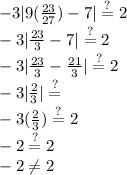
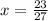`x = (23)/(27)\\` is an extraneous solution.