Answer:
0.02835
Explanation:
Let p be the probability who are in favor of the project and q be the probability who are not in favor of the project.
p = 30% = 0.30
q = 1 - p = 1 - 0.30 = 0.70
n = 5, x = 4
Now, by binomial distribution formula:
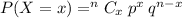
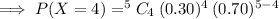
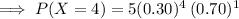
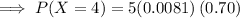
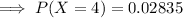
The probability that exactly 4 of them favor the new building project is 0.02835.