Answer:
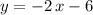 .
.
Explanation:
Calculate the gradient of line
 . For a non-vertical line that goes through
. For a non-vertical line that goes through
 and
and
 where
where
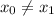 , the gradient would be:
, the gradient would be:
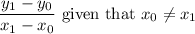 .
.
For line
 , the two points are
, the two points are
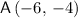 and
and
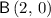 . Hence, the gradient of line
. Hence, the gradient of line
 would be:
would be:
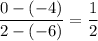 .
.
The perpendicular bisector of a line segment (
 in this question) is perpendicular to that line segment.
in this question) is perpendicular to that line segment.
In a cartesian plane, the gradients of two lines perpendicular to one another would be inverse reciprocals. In other words, the product of these two gradients would be
 .
.
Hence, if
 represents the gradient of
represents the gradient of
 , and
, and
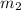 represents the gradient of the perpendicular bisector, then
represents the gradient of the perpendicular bisector, then
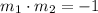 .
.
Since the gradient of
 is
is
 , the gradient of its perpendicular bisector would be:
, the gradient of its perpendicular bisector would be:
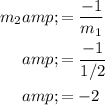 .
.
The perpendicular bisector of a line segment (
 in this question) goes through the midpoint of that line segment.
in this question) goes through the midpoint of that line segment.
Apply the midpoint formula to find the midpoint of segment
 .
.
If the endpoints of a line segment are
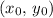 and
and
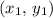 , the midpoint of that line segment would be:
, the midpoint of that line segment would be:
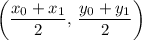 .
.
The two endpoints of segment
 are
are
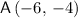 and
and
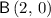 . The midpoint of segment
. The midpoint of segment
 would be:
would be:
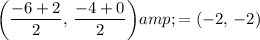 .
.
Find the equation of this perpendicular bisector in the point-slope form.
Consider a non-vertical line of slope
 . If this line goes through the point
. If this line goes through the point
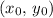 , the point-slope form equation of this line would be:
, the point-slope form equation of this line would be:
 .
.
The slope of the perpendicular bisector in this question is
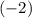 . Besides, this line goes through the point
. Besides, this line goes through the point
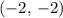 . Henec, the point-slope equation of this line would be:
. Henec, the point-slope equation of this line would be:
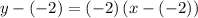 .
.
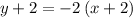 .
.
All the choices in this question are in the slope-intercept form. Hence, rewrite the point-slope equation
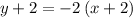 to find the corresponding (equivalent) slope-intercept equation of this line:
to find the corresponding (equivalent) slope-intercept equation of this line:
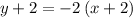 .
.
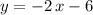 .
.