Question

12. Find a number t such that the line containing the points

(t, -2)and (-3,5) is perpendicular to the line that contains the
points (3,7) and (5, 11).

Answer 1

t= 11

Explanation:

`\boxed{gradient = (y1 - y2)/(x1 - x2) }`

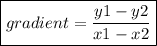
Gradient of line that contains points (3, 7) & (5, 11)

`= (11 - 7)/(5 - 3)`

`= (4)/(2)`

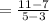
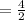
= 2

The product of the gradients of two perpendicular lines is -1.

Gradient of the line that contains points (t, -2) & (-3, 5)

= -1 ÷2

`= - (1)/(2)`

`( - 2 - 5)/(t - ( -3 )) = - (1)/(2)`

`( - 7)/(t + 3) = ( - 1)/(2)`

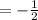
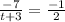
Cross multiply:

-(t +3)= -7(2)

Dividing by -1 on both sides:

t +3= 7(2)

t +3= 14

t= 14 -3

t= 11