Question

Some answer this for me pls

Answer 1

• 120 -x
• x +12

Explanation:

The absolute value function multiplies its argument by -1 if and only if that argument is negative.

a)

`|x-120|=\begin{cases}-(x-120)&\text{for }(x-120) < 0\\(x-120&\text{for }(x-120)\ge0\end{cases}`

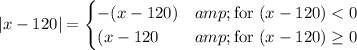
The first condition resolves to ...

x -120 < 0 ⇒ x < 120 . . . . . matches the given condition x < -120

So, we can simplify the expression to ...

-(x -120) = 120 -x . . . when x < -120

__

b)

`|x-(-12)|=\begin{cases}-(x+12)&\text{for }(x+12) < 0\\(x+12)&\text{for }(x+12)\ge0\end{cases}`

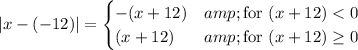
The second condition resolves to ...

x+12 ≥ 0 ⇒ x ≥ -12 . . . . . matches the given condition x > -12

So, we can simplify the expression to ...

x +12 . . . when x > -12

_____

Additional comment

You may have noticed that the function |x -120| translates the absolute value function 120 units to the right. The condition x < -120 puts the boundary at 120 unit to the left of 0, well within the area to the left of the vertex. This is illustrated by the attached graph.