Question

. Solve: - 5x² + 5 = - 2x The solution contains a reduced fraction another reduced

fraction with a radical numerator. What is this fraction with a radical numerator?
a

Answer 1

Consider the given quadratic equation that we have :

`{:\implies \quad \sf -5x^(2)+5=-2x}`

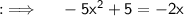
Multiplying both sides by -1 will yield ;

`{:\implies \quad \sf 5x^(2)-5=2x}`

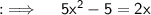
Write the above quadratic equation in the form of standard quadratic equation ax² + bx + c = 0 ,

`{:\implies \quad \sf 5x^(2)-2x-5=0}`

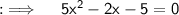
Now , comparing this with the standard form of quadratic equation we will get a = 5 , b = -2 , c = -5 . So now , Discriminant (D) = (-2)² - 4 × 5 × -5 = 4 + 100 = 104

Now , by the quadratic formula ;

`{:\implies \quad \sf x=(-(-2)\pm √(104))/(2* 5)}`

`{:\implies \quad \sf x=(2\pm 2√(26))/(2* 5)}`

`{:\implies \quad \sf x=\frac{\cancel{2}(1\pm √(26))}{\cancel{2}* 5}}`

`{:\implies \quad \bf \therefore \quad \underline{\underline{x=(1\pm √(26))/(5)}}}`

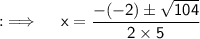
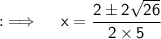
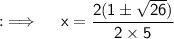
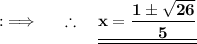
Used Concepts :-

For any quadratic equation of the form ax² + bx + c , the Discriminant (D) is given by D = b² - 4ac , and the root
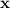`\bf x` of the quadratic equation is given by the quadratic formula as

• 
  `{\boxed{\bf{x=(-b\pm √(D))/(2a)}}}`