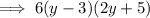Answer:
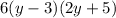
Explanation:
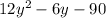
First, factor out the common term of 6:
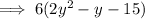
To factor
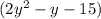 :
:
Multiply the coefficient of
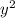 by the constant:
by the constant:
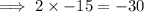
Now find factors of -30 that sum to the coefficient of
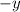 , i.e. -1
, i.e. -1
Factors of 30: 1, 2, 3, 5, 6, 10, 15, 30
So factors of -30 that sum of -1 are: -6 and 5
Rewrite the middle term of
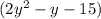 as
as
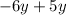 :
:
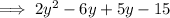
Factor each pair of terms:
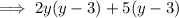
Factor out the constant term:
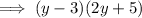
Therefore, the final factorization is: