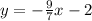Answer:
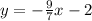
Explanation:
Here, we have to convert the equation to slope-intercept form so we can find the perpendicular slope:
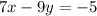
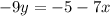
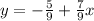
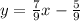
Since our slope is
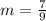 , then that means the slope perpendicular to it is
, then that means the slope perpendicular to it is
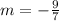 .
.
Now we find our new y-intercept so that the line will pass through the point (-7,7):
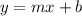
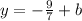
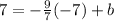
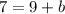
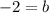
Therefore, the equation of the new line is