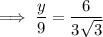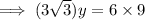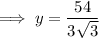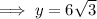Question

What is the value of y?

Answer 1

Apply Pythagorean theorem in ∆TMU

`\\ \rm\Rrightarrow UT^2=6^2-3^2=36-9=27`

`\\ \rm\Rrightarrow UT=3√(3)`

Now

• in ∆TNU

`\\ \rm\Rrightarrow y^2=(3\sqrt)^2+9^2`

`\\ \rm\Rrightarrow y^2=27+81`

`\\ \rm\Rrightarrow y^2=108`

`\\ \rm\Rrightarrow y=6√(3)`

Answer 2

6√3 units

Explanation:

Similar right triangle theorem states that as ΔNUT ≅ ΔTUM then

NT : NU = TM : TU

First find the length of TU using Pythagoras' Theorem: a² + b² = c²

(where a and b are the legs, and c is the hypotenuse, of a right triangle)

⇒ UM² + TU² = TM²

⇒ 3² + TU² = 6²

⇒ TU² = 27

⇒ TU = √(27)

⇒ TU = 3√3

Given:

• NT = y
• NU = 9
• TM = 6
• TU = 3√3

NT : NU = TM : TU

⇒ y : 9 = 6 : 3√3

`\implies (y)/(9)=(6)/(3√(3) )`

`\implies (3√(3))y=6 * 9`

`\implies y=(54)/(3√(3))`

`\implies y=6√(3)`