Check the picture below on the left-hand-side.
we know the degree of the polynomial will be 6, so the exponents of its factors must add up to 6.
now, we know that at -4 and -1 it has an odd multiplicity, so the exponent of that factor could be either 3 or 1 hmmm so which is it?
well, when the graph cross the axis straight through, it'd be a multiplicity of 1, when it leans a bit on the axis, like it does on -4, the multiplicity will be larger than 1, so then
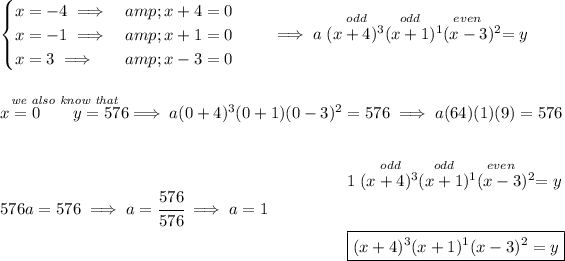
Check the picture below on the right-hand-side