Question

A school fund raising event sold a total of 206 tickets and generated a total revenue of $762.45. There are two types of tickets: adult tickets and child tickets. Each adult ticket costs $5.70, and each child ticket costs $2.65. Write and solve a system of equations to answer the following questions.

_____ adult tickets and _____child tickets were sold

Answer 1

71 adult tickets, 135 child tickets

Explanation:

Let the number of adult and child tickets sold be a and c respectively.

`\textcolor{steelblue}{\text{\textcircled{2} Form and label 2 equations}}`

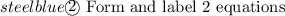
Adult tickets +child tickets= total number of tickets sold

a +c= 206 -----(1)

Revenue from child tickets +revenue from adult tickets= total revenue

Revenue from child tickets

= number of child tickets sold ×cost of each ticket

= 2.65c

Revenue from adult tickets

= number of adult tickets sold ×cost of each adult ticket

= 5.70a

2.65c +5.70a= 762.45 -----(2)

`\textcolor{steelblue}{\text{\textcircled{3} Solve by substitution}}`

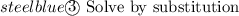
From (1):

a= 206 -c -----(3)

Substitute (3) into (2):

2.65c +5.70(206 -c)= 762.45

Expand:

2.65c +1174.2 -5.70c= 762.45

Simplify:

-3.05c +1174.2= 762.45

-3.05c= 762.45 -1174.2

-3.05c= -411.75

c= -411.74 ÷(-3.05)

c= 135

Substitute c= 135 into (3):

a= 206 -135

a= 71

`\textcolor{steelblue}{\text{\textcircled{4} Concluding statement}}`

Thus, 71 adult tickets and 135 child tickets were sold.