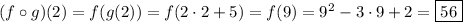Question

Can anyone do these problems it’s for my daughter in law

Answer 1

Classwork:

Given
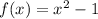`f(x) = x^2 - 1` and
`g(x)=2x+5`, we have

(1)
`(f\circ g)(x) = f(g(x)) = f(2x+5) = (2x+5)^2 - 1 = \boxed{4x^2+20x+24}`

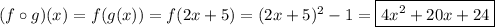
Using the composition found in (1), we have

(2)
`(f\circ g)(-2) = 4\cdot(-2)^2+20\cdot(-2)+24 = \boxed{0}`

(3)
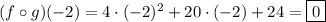
`(g\circ f)(x) = g(f(x)) = g(x^2-1) = 2(x^2-1) + 5 = \boxed{2x^2 + 3}`

Using the composition found in (3),

(4)
`(g\circ f)(1) = 2\cdot1^2+3 = \boxed{5}`

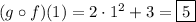
Homework:

Now if
`f(x)=x^2-3x+2`, we would have

(1)
`(f\circ g)(x) = f(2x+5) = (2x+5)^2-3(2x+5)+2 = \boxed{4x^2+14x+12}`

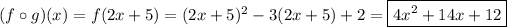
For (2), we could explicitly find
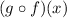`(g\circ f)(x)` then evaluate it at x = -1 like we did in the classwork section, but we don't need to.

(2)
`(g\circ f)(-1) = g(f(-1)) = g((-1)^2-3\cdot(-1)+2) = g(6) = 2\cdot6+5 = \boxed{17}`

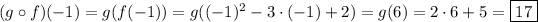
(3) We can demonstrate that both methods work here:

• by using the result from (1),

`(f\circ g)(2) = 4\cdot2^2+14\cdot2+12 = \boxed{56}`

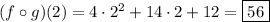
• by evaluating the inner function at x = 2 first,

`(f\circ g)(2) = f(g(2)) = f(2\cdot2+5) = f(9) = 9^2-3\cdot9+2 = \boxed{56}`