Question

A dendrologist measures the height (in feet) of a Mature Red Maple, Big Leaf Maple, Jack Pine, Eastern White Pine, Loblolly Pine, Slash Pine, Longleaf Pine, Black spruce, and Balsam Fir. The recorded heights are given below.

73, 68, 73, 85, 92, 81, 88, 35, 48

Mean
Median
Mode

Answer 1

Solution (Finding the mean of the data):

Step-1: Add the data set.

`\bullet \ \ 73 + 68 + 73 + 85 + 92 + 81 + 88 + 35 + 48`

`\bullet \ \ 643`

Step-2: Divide the "added" data set by the total digits in the data set.

There are nine digits in the data set.

`\bullet \ \ \frac{643}9}`

`\bullet \ \ 71.44`

Thus, the mean of the data set is 71.44.

Solution (Finding the median of the data):

Step-1: Arrange the data set in descending form.

Greatest => Smallest

`\bullet \ \ 73, 68, 73, 85, 92, 81, 88, 35, 48`

`\bullet \ \ 92, 88, 85, 81, 73, 73, 68, 48, 35`

Step-2: Count the number of digits in the data.

`\bullet \ \ \tex\text{9 digits in total}`

Step-3: Revise the following.

`\bullet \ \ \tex\text{If there are even number of digits:} \ \frac{\tex\text{(Number of digits)}}{2}`

`\bullet \ \ \tex\text{If there are odd number of digits:} \ \frac{\tex\text{(Number of digits)} + 1}{2}`

Step-4: Odd or Even?

`\bullet \ \ \tex\text{Even numbers:} \ 2, 4, 6, 8, 10...`

`\bullet \ \ \tex\text{Odd numbers:} \ \ 1, 3, 5, 7, \bold{9}, 11...`

There is an odd number of digits.

Step-5: Use the formula.

`\bullet \ \ \frac{\tex\text{(Number of digits)} + 1}{2}`

`\bullet \ \ \frac{\tex\text{9} + 1}{2}`

`\bullet \ \ \frac{\tex\text{10}}{2}`

`\bullet \ \ 5`

The fifth digit in the data is the median.

Step-6: Revise the data set.

`\bullet \ \ 92, 88, 85, 81, \bold{73}, 73, 68, 48, 35`

The median is 73.

Solution (Finding the mode of the data set:

The most repeating number is the mode. Let's put the data set in a frequency table.

Step-1: Putting the data set in a frequency table:

~Table attached

Looking at the table, we can tell that 73 has repeated two times and has repeated the most.

The mode is 73.

Answer 2

Given set ⤵️

73, 68, 73, 85, 92, 81, 88, 35, 48

Mean ↯

`\boxed{ \tt \: mean = (sum \: of \: observations)/(total \: number \: of \: observations) }`

• Total number of observations = 9

`\sf \rightarrowtail \: mean = (73 + 68 + 73 + 85 + 92 + 81 + 88 + 35 + 48)/(9)`

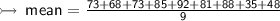
To make the calculation easier, first add the numbers that sum to multiples of 10

`\sf \rightarrowtail \: mean = (643)/(9) = 71.4`

`\red{⊱─━━━━━━━━⊱༻●༺⊰━━━━━━━━─⊰}`

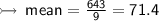
Median ↯

35, 48, 68, 73, 73, 81, 85, 88, 92

`\boxed{ \tt \: median = ( (n + 1)/(2) ) ^(th) \: term }`

• n is the number of observations I.e. 9 in our case

`\sf \multimap \: median = ((9 + 1)/(2) )^(th) \: term`

`\sf \multimap \: median = ((10)/(2) )^(th) \: term`

`\sf \multimap \: median = 5^(th) \: term`

`\sf \multimap \: median = 73`

`\red{⊱─━━━━━━━━⊱༻●༺⊰━━━━━━━━─⊰}`

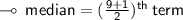
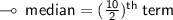
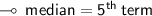
Mode ↯

35, 48, 68, 73, 73, 81, 85, 88, 92

• The most occurred number is 73 it has occurred 2 times. Hence, it is the mode!