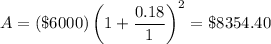Explanation:
The formula for compounded interest is given by
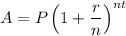
where
A = amount of money after a time t
P = principal or initial amount of money
r = interest rate in decimal form
n = number of times money bnb is compounded per unit time
t = unit time
a) For this problem, P = $6000, n = 1 since the money is compounded once a year, t = 1 year and r = 0.18 so after one year, Lisa's money amounts to
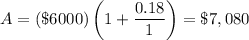
b) After two years, the money is still compounded yearly so n = 1 but t = 2 years so Lisa's money amounts to