Answer:
 .
.
Explanation:
Start by finding the intersection of the two curves:
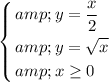 .
.
 while
while
 .
.
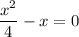 .
.
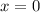 or
or
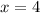 .
.
Therefore, these two curves would intersect at two points:
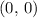 and
and
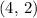 .
.
The area bounded between
 and
and
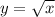 would be between
would be between
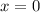 and
and
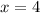 .
.
Refer to the diagram attached. The graph
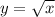 is always above the graph of
is always above the graph of
 over the entire bounded area (except for the two intersections).
over the entire bounded area (except for the two intersections).
Therefore,
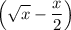 would represent the vertical distance between the upper and lower curve for any given
would represent the vertical distance between the upper and lower curve for any given
 over this bounded area (where
over this bounded area (where
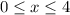 .)
.)
Integrating height over the horizontal variable
 over some closed interval would give area. Likewise, the area between the two curves in this question could be found with the following integral:
over some closed interval would give area. Likewise, the area between the two curves in this question could be found with the following integral:
![\begin{aligned}& \int\limits_(0)^(4) \left(√(x) - (x)/(2)\right)\, dx \\ = \; & \int\limits_(0)^(4) \left(x^(1/2) - (x)/(2)\right)\, dx \\ =\; & \left[(2)/(3)\, x^(3/2) - (x^(2))/(4)\right]_(x=0)^(x=4) \\ =\; & (2* 8)/(3) - 4 \\ =\; &(4)/(3) \end{aligned}](https://img.qammunity.org/2022/formulas/mathematics/college/esq38q4ertqmg0l4a2bkoootulyc9kbruq.png) .
.