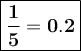
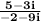
Multiply both numerator and denominator of
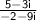 by the complex conjugate of the denominator, -2+9i.
by the complex conjugate of the denominator, -2+9i.
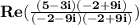
Multiplication can be transformed into difference of squares using the rule:
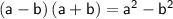 .
.
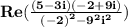
By definition, i² is -1. Calculate the denominator.
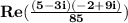
Multiply complex numbers 5-3i and -2+9i in the same way as you multiply binomials.
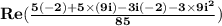
Do the multiplications in
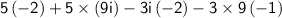 .
.
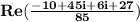
Combine the real and imaginary parts in -10+45i+6i+27.
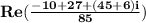
Do the additions in
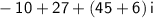 .
.
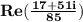
Divide 17+51i by 85 to get
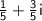 .
.
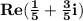
The real part of
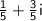 is
is
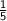 .
.