Question

Perform the indicated operations. Write the answer in standard form, a+bi.

(√3 - √10i) (√3 + √10i)

Answer 1

`\boxed{\underline{\bf \: ANSWER}}`

`\sf( \sqrt { 3 } - 10 i ) ( \sqrt { 3 } + 10 i )`

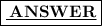
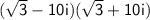
Apply the distributive property by multiplying each term of
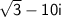`\sf √(3)-10i` by each term of
`\sf√(3)+10i`.

`\sf\left(√(3)\right)^(2)+10i√(3)-10i√(3)+100`

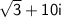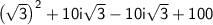
The square of
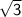`\sf√(3)` is 3.

`\sf3+10i√(3)-10i√(3)+100`

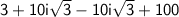
Combine 10i
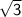`\sf√(3)` and -10i
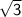`\sf√(3)` to get 0.

`\sf \: 3+100`

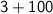
Add 3 and 100 to get 103.

`= \boxed{ \bf \: 103}`

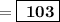
Attachment picture -> the answer shown by an online calculator (103 is the correct answer).

_______

Hope it helps.

ꋪꍏꀤꈤꌃꂦꅏꌗꍏ꒒꓄2222