Question

A car travels a distance of 100 km. For the first 30 minutes it is driven at a constant speed of 80 km/hr. The motor begins to vibrate and the driver reduces the speed to 40 km/hr for the rest of the trip. The average speed for the entire trip is

Answer 1

Step-by-step explanation:

First, we need to determine the distance traveled by the car in the first 30 minutes,
`d_{(1)/(2)}`.

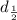Notice that the unit measurement for speed, in this case, is km/hr. Thus, a unit conversion of from minutes into hours is required before proceeding with the calculation, as shown below

`d_{(1)/(2)\text{h}} \ = \ \text{speed} \ * \ \text{time taken} \\ \\ \\ d_{(1)/(2)\text{h}} \ = \ 80 \ \text{km h}^(-1) \ * \ \left(\displaystyle(30)/(60) \ \text{h}\right) \\ \\ \\ d_{(1)/(2)\text{h}} \ = \ 80 \ \text{km h}^(-1) \ * \ 0.5 \ \text{h} \\ \\ \\ d_{(1)/(2)\text{h}} \ = \ 40 \ \text{km}`

Now, it is known that the car traveled 40 km for the first 30 minutes. Hence, the remaining distance,
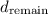`d_{\text{remain}}` , in which the driver reduces the speed to 40km/hr is

`d_{\text{remain}} \ = \ 100 \ \text{km} \ - \ 40 \ \text{km} \\ \\ \\ d_{\text{remain}} \ = \ 60 \ \text{km}`.

Subsequently, we would also like to know the time taken for the car to reach its destination, denoted by
`t_{\text{remian}}`.

`t_{\text{remain}} \ = \ \displaystyle\frac{\text{distance}}{\text{speed}} \\ \\ \\ t_{\text{remain}} \ = \ \displaystyle\frac{60 \ \text{km}}{40 \ \text{km hr}^(-1)} \\ \\ \\ t_{\text{remain}} \ = \ 1.5 \ \text{hours}`.

Finally, with all the required values at hand, the average speed of the car for the entire trip is calculated as the ratio of the change in distance over the change in time.

`\text{speed} \ = \ \displaystyle(\Delta d)/(\Delta t) \\ \\ \\ \text{speed} \ = \ \displaystyle\frac{100 \ \text{km}}{(0.5 \ \text{hr} \ + \ 1.5 \ \text{hr})} \\ \\ \\ \text{speed} \ = \ \displaystyle\frac{100 \ \text{km}}{2 \ \text{hr}} \\ \\ \\ \text{speed} \ = \ 50 \ \text{km hr}^(-1)`

Therefore, the average speed of the car is 50 km/hr.