Question

38. Evaluate f (3x +4y)dx + (2x --3y)dy where C, a circle of radius two with center at the origin of the xy

C plane, is traversed in the positive sense.

please i need real time help

Answer 1

It looks like the integral is

`\displaystyle \int_C (3x+4y)\,\mathrm dx + (2x-3y)\,\mathrm dy`

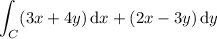
where C is the circle of radius 2 centered at the origin.

You can compute the line integral directly by parameterizing C. Let x = 2 cos(t ) and y = 2 sin(t ), with 0 ≤ t ≤ 2π. Then

`\displaystyle \int_C (3x+4y)\,\mathrm dx + (2x-3y)\,\mathrm dy = \int_0^(2\pi) \left((3x(t)+4y(t))(\mathrm dx)/(\mathrm dt) + (2x(t)-3y(t))(\mathrm dy)/(\mathrm dt)\right)\,\mathrm dt \\\\ = \int_0^(2\pi) \big((6\cos(t)+8\sin(t))(-2\sin(t)) + (4\cos(t)-6\sin(t))(2\cos(t))\big)\,\mathrm dt \\\\ = \int_0^(2\pi) (12\cos^2(t)-12\sin^2(t)-24\cos(t)\sin(t)-4)\,\mathrm dt \\\\ = 4 \int_0^(2\pi) (3\cos(2t)-3\sin(2t)-1)\,\mathrm dt = \boxed{-8\pi}`

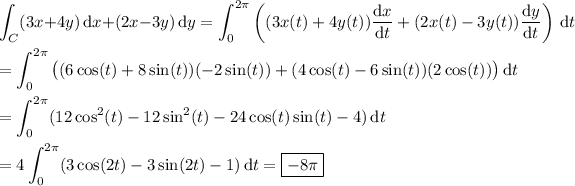
Another way to do this is by applying Green's theorem. The integrand doesn't have any singularities on C nor in the region bounded by C, so

`\displaystyle \int_C (3x+4y)\,\mathrm dx + (2x-3y)\,\mathrm dy = \iint_D(\partial(2x-3y))/(\partial x)-(\partial(3x+4y))/(\partial y)\,\mathrm dx\,\mathrm dy = -2\iint_D\mathrm dx\,\mathrm dy`

where D is the interior of C, i.e. the disk with radius 2 centered at the origin. But this integral is simply -2 times the area of the disk, so we get the same result:
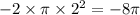`-2* \pi*2^2 = -8\pi`.