Answer:
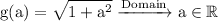
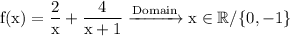
Explanation:
Question-1:
we want to figure out the domain of the following function:
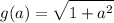
remember that, the domain of an even root function are all values of x for which the redicand is positive or 0 that is being said the domain of the function g(a) belong to
 . another way to think about it, the domain of square root function f(x) belong to x≥0. In this case we have square variable in the redical so when we input a negative number, it yields a positive number with that said the domain of the function g(a) belong to all the real numbers.Thus,
. another way to think about it, the domain of square root function f(x) belong to x≥0. In this case we have square variable in the redical so when we input a negative number, it yields a positive number with that said the domain of the function g(a) belong to all the real numbers.Thus,
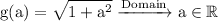
Question-2:
we'd like to find the domain of the following function:
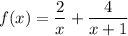
in order to do so we need to simplify it further,so simplify addition in order to do so the first step is to figure out the LCM of the denominator i.e x(x+1) ⇒ x²+x, secondly divide the denominator of every fraction by the LCM and multiply the result by the numerator of very fraction ,then finally add them therefore,
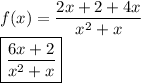
we know that the domain of a rational function are all the values of x for which the denominator is different than 0.
the denominator of the function would be 0 when x=0 and -1 thus,
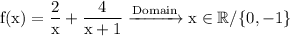
and we're done!