Question

Evaluate the logarithm at the given value of x without using a calculator.

Function Value
g(x) = log_b(x) x = √b

Answer 1

9514 1404 393

Answer:

g(x) = 1/2

Explanation:

The applicable relations are ...

`\log_b(x)=a\ \Longleftrightarrow\ b^a=x\\\\\log_b(x^a)=a\cdot\log_b(x)\\\\\log_b(b)=1`

__

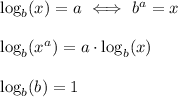
We want to find logb(x) for x = b^(1/2). Using the first relation, we see ...

g(x) = logb(x)

b^(g(x)) = b^(1/2) . . . . . using g(x) = a

g(x) = 1/2 . . . . . equating exponents

__

Alternatively, using the last two relations, we have x = b^(1/2), so ...

g(b^(1/2)) = logb(b^(1/2)) = (1/2)logb(b) = (1/2)(1)

g(x) = 1/2

_____

Additional comment

I find it useful to remember that a logarithm is an exponent. The first applicable relation shown above is a statement to that effect.