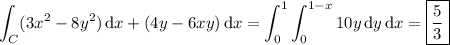I'll only look at (37) here, since
• (38) was addressed in 24438105
• (39) was addressed in 24434477
• (40) and (41) were both addressed in 24434541
In both parts, we're considering the line integral
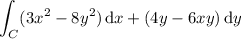
and I assume C has a positive orientation in both cases
(a) It looks like the region has the curves y = x and y = x ² as its boundary***, so that the interior of C is the set D given by

• Compute the line integral directly by splitting up C into two component curves,
C₁ : x = t and y = t ² with 0 ≤ t ≤ 1
C₂ : x = 1 - t and y = 1 - t with 0 ≤ t ≤ 1
Then

*** Obviously this interpretation is incorrect if the solution is supposed to be 3/2, so make the appropriate adjustment when you work this out for yourself.
• Compute the same integral using Green's theorem:
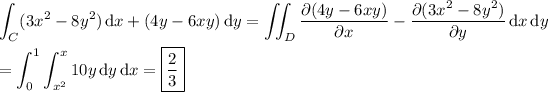
(b) C is the boundary of the region

• Compute the line integral directly, splitting up C into 3 components,
C₁ : x = t and y = 0 with 0 ≤ t ≤ 1
C₂ : x = 1 - t and y = t with 0 ≤ t ≤ 1
C₃ : x = 0 and y = 1 - t with 0 ≤ t ≤ 1
Then
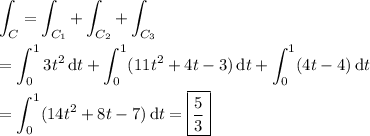
• Using Green's theorem: