Question

Please help me with this. thanks a lot​

Answer 1

Part A)

Approximately 318.1318 meters.

Part B)

Approximately 137.7551 meters.

Explanation:

The path of a projectile is given by the equation:

`\displaystyle y = √(3) x -(49x^2)/(9000)`

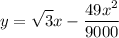
Part A)

The range of the projectile will be given by the difference between its starting point and landing point. In other words, its two zeros.

Let y = 0 and solve for x:

`\displaystyle 0 = √(3)x - (49x^2)/(9000)`

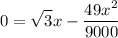
Factor:

`\displaystyle 0 = x\left(√(3) - (49x)/(9000)\right)`

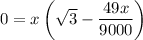
Zero Product Property:

`\displaystyle x = 0 \text{ or } √(3) - (49x)/(9000) = 0`

Solve for each case:

`\displaystyle x = 0 \text{ or } x = (9000√(3))/(49)\approx 318.1318`

Hence, the range of the projectile is approximately (318.1318 - 0) or 318.1318 meters.

Part B)

Since the equation is a quadratic, the maximum height is given by its vertex. Recall that the vertex of a quadratic is given by:

`\displaystyle \text{Vertex} = \left(-(b)/(2a), f\left(-(b)/(2a)\right)\right)`

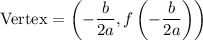
In this case, a = -49/9000 and b = √3.

Find the x-coordinate of the vertex:

`\displaystyle x = - ((√(3)))/(2\left((-49)/(9000)\right)) = (4500√(3))/(49)`

Then the maximum height will be:

`\displaystyle \displaystyle \begin{aligned} y\left((4500√(3))/(49)\right) &=√(3) \left((4500√(3))/(49)\right) -(49\left((4500√(3))/(49)\right)^2)/(9000) \\ \\ &= (13500)/(49) -(6750)/(49)\\ \\ &=(6750)/(49)\\ \\ &\approx 137.7551\text{ meters}\end{aligned}`

The maximum height reached by the projectile will be 137.7551 meters.