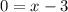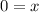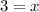Answer:
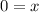 ,
,
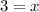
Explanation:
One is given the following equation:
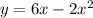
Factor this expression:
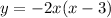
Set the equation equal to (0), then use the zero-product property to solve for (x). The zero product property states that any number times zero equals zero. Thus, one can apply this here to solve for (x):
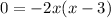

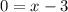
Inverse operations,