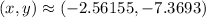Question

Please help! Solve this question

Answer 1

The two points of intersection are approximately (-2.56155, -7.3693) and (1.56155, 17.3693)

==========================================================

Step-by-step explanation:

Apply substitution and get everything to one side

`y = 6x+8\\\\x^2+7x+4 = 6x+8\\\\x^2+7x+4-6x-8 = 0\\\\x^2+x-4 = 0\\\\`

Now apply the quadratic formula with a = 1, b = 1, c = -4

`x = (-b\pm√(b^2-4ac))/(2a)\\\\x = (-1\pm√((1)^2-4(1)(-4)))/(2(1))\\\\x = (-1\pm√(1+16))/(2)\\\\x = (-1\pm√(17))/(2)\\\\x = (-1+√(17))/(2) \ \text{ or } \ x = (-1-√(17))/(2)\\\\x \approx 1.56155\ \text{ or } \ x \approx -2.56155\\\\`

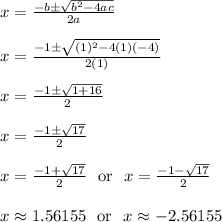
Each approximate x value is then plugged into either original equation to find its corresponding paired y value.

Let's plug the first x value found.

`y = 6x+8\\\\y \approx 6(1.56155)+8\\\\y \approx 17.3693\\\\`

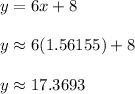
Therefore
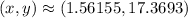`(x,y) \approx (1.56155, 17.3693)` is one approximate point of intersection.

Repeat for the other x value

`y = 6x+8\\\\y = 6(-2.56155)+8\\\\y = -7.3693\\\\`

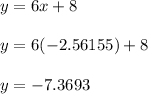
The other point of intersection is roughly located at
`(x,y) \approx (-2.56155, -7.3693)`