Question

Find the values of x and y.

Answer 1

`\bold{\huge{\underline{ Solution }}}`

Let consider the given triangle be ABC

According to the question,

AD is the median of the triangle ABC and CE also divides the triangle into two parts. At F both the lines are intersecting.

Here We have ,

• 
  `\sf{\angle{ EAF = 25{\degree}}}`
• 
  `\sf{\angle{ AEF = x{\degree}}}`
• 
  `\sf{\angle{ EBD = y {\degree}}}`
• 
  `\sf{\angle{ FDC = 90{\degree}}}`
• 
  `\sf{\angle{ DCF = 20{\degree}}}`

In triangle FDC, By using Angle sum property

`\sf{ {\angle}FDC + {\angle}DCF + {\angle}CFD = 180{\degree}}`

Subsitute the required values,

`\sf{ 90{\degree} + 20{\degree} + {\angle}CFD = 180{\degree}}`

`\sf{ 110{\degree} + {\angle}CFD = 180{\degree}}`

`\sf{ {\angle}CFD = 180{\degree} - 110{\degree}}`

`\sf{ {\angle}CFD = 70{\degree}}`

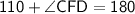
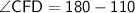
Here.

• 
  `\sf{ {\angle}CFD = {\angle}EFA = 70{\degree}}`
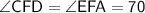
• The above angles are vertically opposite angles and vertically opposite angles are equal.

Now, Again by using Angle sum property but in triangle AEF

`\sf{ {\angle}AEF + {\angle}EFA + {\angle}FAE = 180{\degree}}`

Subsitute the required values,

`\sf{ x{\degree} + 70{\degree} + 25{\degree} = 180{\degree}}`

`\sf{ x{\degree} + 95{\degree}= 180{\degree}}`

`\sf{ x{\degree} = 180{\degree} - 95{\degree}}`

`\bold{ x = 85{\degree}}`

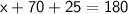
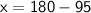
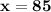
Thus , The value of x is 85°

• Here, In the triangle ABC , CE divides the triangle into two parts

So ,

`\sf{ {\angle}AEF + {\angle}FEB = 180{\degree}}`

`\sf{ 85{\degree} + {\angle}FEB = 180{\degree}}`

`\sf{ {\angle}FEB = 180{\degree} - 85{\degree}}`

`\sf{ {\angle}FEB = 95{\degree}}`

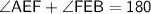
Similarly ,

`\sf{ {\angle}AFE + {\angle}DFE = 180{\degree}}`

• Straight line angles

`\sf{ 70{\degree} + {\angle}DFE = 180{\degree}}`

`\sf{ {\angle}DFE = 180{\degree} - 70{\degree}}`

`\sf{ {\angle}DFE = 110 {\degree}}`

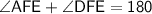
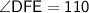
• In triangle ABC, EBDF is forming quadrilateral

We know that,

• Sum of all the angles of quadrilateral is equal to 360°

That is ,

`\sf{ {\angle}FEB + {\angle}EBD + {\angle}BDF + {\angle} DFE = 360{\degree}}`

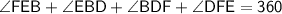
Subsitute the required values,

`\sf{ 95{\degree} + y{\degree} + 90{\degree} + + 110{\degree} = 360{\degree}}`

`\sf{ y{\degree} + 295{\degree}= 180{\degree}}`

`\sf{ y {\degree} = 360{\degree} - 295{\degree}}`

`\bold{ y = 65{\degree}}`

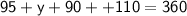
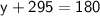
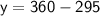
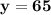
Hence, The value of x and y is 70° and 65° .