Answer:
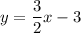
Explanation:
Hi there!
Slope-intercept form:
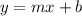 where m is the slope and b is the y-intercept (the value of y when x=0)
where m is the slope and b is the y-intercept (the value of y when x=0)
We're given:
⇒ x-intercept = 2
⇒ y-intercept = -3
1) Determine the slope (m)
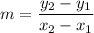 where two points that fall on the line are
where two points that fall on the line are
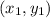 and
and
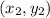
Given the x- and y-intercepts, we can rewrite them as points:
x-intercept = 2
⇒ (2,0)
y-intercept = -3
⇒ (0,-3)
Plug these points into the equation:
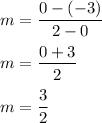
Therefore, the slope of the line is
 . Plug this into
. Plug this into
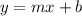 :
:
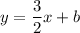
2) Plug in the y-intercept (b)
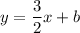
We're given the y-intercept: -3. Plug this into
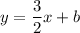 :
:
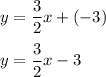
I hope this helps!