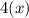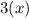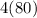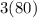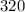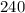Question

Help whhhahahahaha Helpppppppp
​

Answer 1

320/420 = 4/3

Explanation:

4/7= x /560

Cross multiply

7x = 2240

Divide by 7:

x=320

The school has 320 boys and 240 girls

I hope this helps u:)

Answer 2

Problem(1):
`21`

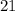
Problem(2): Side length =
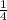`(1)/(4)` Area =
`(1)/(16)`

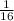
Problem(3): Boys =
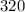`320` Girls =
`240`

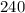
Explanation:

(Notes steps are cut from this answer so that it isn't too long)

1. Problem (1)

One is given the following information:

• 
  `x+(1)/(x)=5`

• 
  `(x-(1)/(x))^2`

The most logical first step is to solve for the value of (x). One can solve for the numerical value of (x) with the first equation.

`x+(1)/(x)=5`

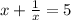
Multiply the entire equation by (x),

`x^2+1=5x`

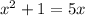
Inverse operations put the equation in the general format of a quadratic equation. The general format of a quadratic equation is as follows,

`ax^2+bx+c=0`

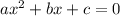
Put the given equation in this format,

`x^2-5x+1=0`

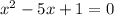
Now use the quadratic formula to solve for the value of (x). The quadratic formula uses the coefficients of the terms in a quadratic equation to find the roots of the equation. The quadratic formula is as follows,

`(-b(+-)√(b^2-4ac))/(2a)`

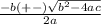
Use the coefficients of the terms in the given quadratic equation in the formal, then simplify to solve for solutions of the given equation,

`(-(-5)(+-)√((-5)^2-4(1)(1)))/(2(1))`

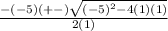
Simplify,

`(-(-5)(+-)√((-5)^2-4(1)(1)))/(2(1))`

`(5(+-)√(21))/(2)`

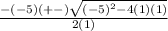
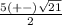
Now substitute these values into the equation and simplify, even though there are two values of (x), there will only be one solution,

`(((5+√(21))/(2)-(1)/((5+√(21))/(2)))^2`
`(((5-√(21))/(2)-(1)/((5-√(21))/(2)))^2`

`((5+√(21))/(2)-(2)/(5+√(21)))^2`
`((5-√(21))/(2)-(2)/(5-√(21)))^2`

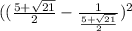
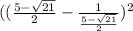
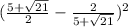
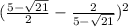
Convert to a common denominator,

`((5+√(21))/(2)*(5+√(21))/(5+√(21))-(2)/(5+√(21))*(2)/(2))^2`
`((5-√(21))/(2)*(5-√(21))/(5-√(21))-(2)/(5-√(21))*(2)/(2))^2`

`(((5+√(21))^2-4)/(2(5+√(21))))^2`
`(((5-√(21))^2-4)/(2(5-√(21))))^2`

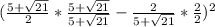
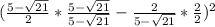
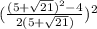
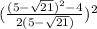
Simplify,

`((25+10√(21)+21-4)/(10+2√(21)))^2`
`((25-10√(21)+21-4)/(10-2√(21)))^2`

`((42+10√(21))/(10+2√(21)))^2`
`((42-10√(21))/(10-2√(21)))^2`

`(1764+840√(21)+2100)/(100+40√(21)+84)`
`(1764-840√(21)+2100)/(100-40√(21)+84)`

`(3864+840√(21))/(184+40√(21))`
`(3864-840√(21))/(184-40√(21))`

`21`

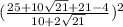
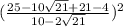
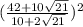
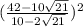
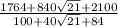
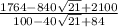
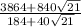
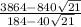
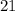
2. Problem (2)

All four sides of a square are congruent (have the same measure), thus dividing the perimeter of a square by (4) will yield the side length of the square,

`Perimeter\ of\ the\ square: 4\\Side\ length: (1)/(4)`

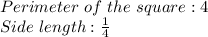
The area is the two-dimensional space that a figure takes up, in the case of a square, the area is the side length times itself:

`A=((1)/(4))^2=(1)/(16)`

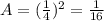
3. Problem (3)

Let (x) represent the amount by which the ratio of boys to girls was scaled down. Assuming that these are the only two genders in the school, one can state that the sum ratio coefficients times the scaling value for both boys and girls, will equal the total number of people in the school. Thus, one can form the following equation and solve it with inverse operations and simplification,

`boys + girl = total\ students\\4x + 3x = 560\\7x = 560\\x = 80`

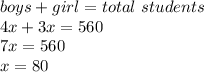
Now substitute this into the expression for the two genders in this scenario, respectively, to solve for the actual number of students of that gender,

Boys, Girls,

`4(x)`
`3(x)`

`4(80)`
`3(80)`

`320`
`240`