Answer:

Explanation:
We want to determine the equation of the line that passes through the point (3, 4) and is parallel to the line containing the points (3, 5) and (0, 2).
Recall that parallel lines have equivalent slopes.
Hence, first find the slope of the line containing the points (3, 5) and (0, 2):
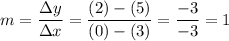
Therefore, the slope of our new line must also be 1.
We are given that it passes through the point (3, 4). Since we are given a slope and a point, we can consider using point-slope form:
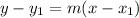
Substitute:
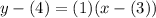
Simplify:
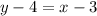
And add. Hence, our equation in slope-intercept form is:

In conclusion, the line that passes through the point (3, 4) and is parallel to the line containing the two points (3, 5) and (0, 2) is:
