Question

NO LINKS!!!

Use the graph of f(x) below to determine the following. Please help me. ​

Answer 1

Answers:

• a) Domain =
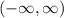  `(-\infty, \infty)` and Range =
  `(-\infty, 4]`
• b) x intercepts = (-4,0) and (4,0); y intercept = (0,1)
• c)
  `(-2, 0) \cup (3,\infty)`
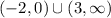
• d)
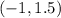  `(-1, 1.5)` which is interval notation; not ordered pair notation
• e)
  `(-\infty, -4] \cup [4,\infty)`
• f) (-2,4) and (0,1) and (3,2)
• g) No, the function is not odd.
• h) f(f(-2)) = 0

=======================================================

Step-by-step explanation:

a)

The domain is the set of allowed x inputs. The graph spans forever to the left and to the right, meaning the set of all real numbers is the domain. We can write that as an inequality like this
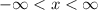`-\infty < x < \infty` which becomes the interval notation
`(-\infty, \infty)`

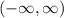
The range is the set of possible y outputs of a function. The highest y can go is y = 4 shown by the mountain peak on the left side at (-2,4). The range as an inequality is
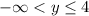`-\infty < y \le 4` which becomes the interval notation
`(-\infty, 4]`

The use of a square bracket means we include the endpoint 4.

---------------------

b)

The x intercepts are the locations where the function curve crosses the x axis. That would be at the locations (-4,0) and (4,0).

The y intercept is where the graph crosses the y axis and it is at (0,1)

---------------------

c)

A decreasing function slopes downhill when moving to the right.

For this f(x) function, such a thing occurs on the interval -2 < x < 0 and on the interval 3 < x < infinity.

Those translate over to the interval notation of
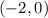`(-2,0)` and
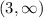`(3, \infty)` respectively. Use the union symbol to glue the intervals together getting the final result of
`(-2,0) \cup (3,\infty)`

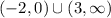
That notation says "x is in the interval -2 < x < 0, or it is in the interval 3 < x < infinity".

---------------------

d)

I'm not sure how to do this without knowing what the function is (eg: something like f(x) = -x^4+5x). The graph alone isn't enough to accurately pinpoint the locations of concave down vs concave up.

We'll have to eyeball it. The portion on the interval -infinity < x < -1 appears to be concave down. Then we have -1 < x < 1.5 or so appear to be concave up. Then finally 1.5 < x < infinity seems to be concave down.

The -1 < x < 1.5 then translates to the interval notation
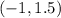`(-1, 1.5)` which is not to be mixed up with ordered pair notation. Unfortunately the two notations look identical sometimes.

---------------------

e)

The graph is on or below the x axis for the intervals of:

• -infinity < x ≤ -4
• 4 ≤ x < infinity

Those lead directly to the interval notation
`(-\infty, -4] \cup [4, \infty)`

I'm using square brackets to include the endpoints -4 and 4. Like with part c, the union symbol U represents the word "or" pretty much. Either we're in one interval or the other, but not both.

---------------------

f)

The critical points are where the graph changes direction. These represent vertex points, which are either the highest or lowest of a given neighborhood.

The graph shows we have three such points:

• (-2,4)
• (0,1)
• (3,2)

The first and last points are local maxes, and the middle point mentioned is a local min.

---------------------

g)

We have f(x) not being odd because the graph does not go through the origin. All odd functions must go through the origin. This is possibly the quickest way to rule out f(x) being odd.

Another way is to show that f(-x) = -f(x) is false for any counter-example.

For instance, if x = 2 then f(-x) = f(-2) = 4 while -f(x) = -f(2) = some value between 1 and 2. So it's hopefully fairly clear that f(-2) = -f(2) is false which means f(-x) = -f(x) is false in general.

---------------------

h)

f(-2) = 4 according to the graph, due to the point (-2,4)

From here we can say

f(f(-2)) = f(4) = 0