Question

1+sin^4-cos^4a/1-sin^6-cos^6a=2/3cos^2a​

Answer 1

Explanation:

From what I can come up with with no actual factual information is that the equation is

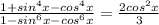`(1+sin^4x-cos^4x)/(1-sin^6x-cos^6x)=(2cos^2x)/(3)` I'm going with that because it actually solves pretty easily, which is usually the way this goes. Begin by cross multiplying:

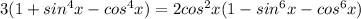`3(1+sin^4x-cos^4x)=2cos^2x(1-sin^6x-cos^6x)` and distribute:

`3+3sin^4x-3cos^4x=2cos^2x-2cos^2xsin^6x-2cos^8x` and then break up the powers of sin into squared sines:

`3+3[sin^2x*sin^2x]-3cos^4x=2cos^2x-2cos^2x[sin^2x*sin^2x*sin^2x]-2cos^8x` and use the Pythagorean identity to change those sines into cosines:

`3+3[(1-cos^2x)(1-cos^2x)]-3cos^4x=2cos^2x-2cos^2x[(1-cos^2c)(1-cos^2x)(1-cos^2x)]-2cos^8x`

and the FOIL out those terms inside the square brackets:

`3+3[1-2cos^2x+cos^4x]-3cos^4x=2cos^2x-2cos^2x[1-3cos^2x+3cos^4x-cos^6x]-2cos^8x`

and distribute again on both sides to get rid of the brackets entirely:

`3+3-6cos^2x+3cos^4x-3cos^4x=2cos^2x-2cos^2x+6cos^4x-6cos^6x+2cos^8x-2cos^8x`

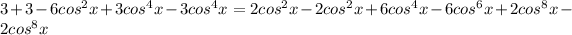
and combining like terms cancels a lot of that out to leave:

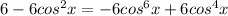`6-6cos^2x=-6cos^6x+6cos^4x` and get everything on one side to factor:

`0=-6cos^6x+6cos^4x+6cos^2x-6` and factor out the -6:

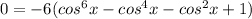`0=-6(cos^6x-cos^4x-cos^2x+1)` and now we'll factor by grouping, so grouping everything together to get ready for that:

`0=-6[(cos^6x-cos^4x)-(cos^2x+1)]` and begin the factoring:

`0=6[cos^4x(cos^2x-1)-1(cos^2x-1)]` and continuing the factoring:

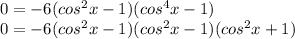`0=-6(cos^2x-1)(cos^4x-1)\\0=-6(cos^2x-1)(cos^2x-1)(cos^2x+1)` and by the Zero Product Property (and we won't list that duplicated factor cuz it's not necessary):

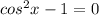`cos^2x-1=0` or
`cos^2x+1=0`

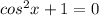
Solving the first:

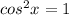`cos^2x=1` so

x = 0 + 2kπ and solving the second one:

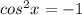`cos^2x=-1` which is not solvable over the real number system.

So x = 0 + 2kπ

and I really hope that's what you were looking for!