Question

Identify the equation of the circle that has its center at (9, 12) and passes through the origin.

Answer 1

Answer:
`(x-9)^2 + (y-12)^2 = 225\\\\`

This is the same as writing (x-9)^2 + (x-12)^2 = 225

========================================================

Step-by-step explanation:

Any circle equation fits the template of
`(x-h)^2 + (y-k)^2 = r^2\\\\`

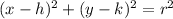
The center is (9,12) which tells us the values of h and k in that exact order.

h = 9

k = 12

To find the radius r, we need to find the distance from the center (9,12) to a point on the circle. The only point we know on the circle is the origin (0,0).

Apply the distance formula to find the distance from (9,12) to (0,0)

`d = √( (x_1-x_2)^2+(y_1-y_2)^2)\\\\d = √( (9-0)^2+(12-0)^2)\\\\d = √( (9)^2+(12)^2)\\\\d = √( 81+144)\\\\d = √( 225)\\\\d = 15\\\\`

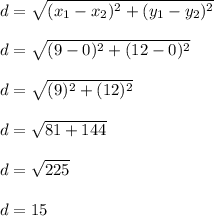
The distance from (9,12) to (0,0) is 15 units. Therefore, r = 15

An alternative to finding this r value is to apply the pythagorean theorem. The distance formula is effectively a modified version of the pythagorean theorem.

---------------------

Since h = 9, k = 12 and r = 15, we can then say:

`(x-h)^2 + (y-k)^2 = r^2\\\\(x-9)^2 + (y-12)^2 = 15^2\\\\(x-9)^2 + (y-12)^2 = 225\\\\`

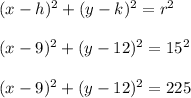
which is the equation of this circle.