Question

Find a general expression for y given that

a
dy
-
=
9x – 2
3x
dx


I need help with either question 2 or 3 please!

Answer 1

We need to solve two questions first from differential equations and the second one from Integral Calculus, but before starting let's recall the formulae and concepts which will help us a lot in doing the questions:

• 
  `{\boxed{\displaystyle \bf \int x^(n)\:dx=(x^(n+1))/(n+1)+C\:\: , \:\: n\\eq -1}}`

• 
  `{\boxed{\displaystyle \bf \int \{f(x)\pm g(x)\pm h(x)\pm \cdots\}dx=\int f(x)\: dx\pm \int g(x)\:dx\pm \int h(x)\:dx\pm \cdots}}`

• 
  `{\boxed{\displaystyle \bf \int kf(x)\:dx=k\int f(x)\:dx}}`

• 
  `{\boxed{\displaystyle \bf \int dx=x+C}}`

Where , C is the Arbitrary Constant and k being any constant

Question 1 :-

Consider the differential equation :-

`{:\implies \quad \sf (dy)/(dx)=(9x-2)/(3√(x))}`

`{:\implies \quad \sf dy=(9x-2)/(3√(x))dx}`

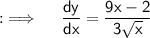
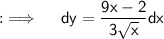
Seperate the denominators of the fraction in RHS

`{:\implies \quad \sf dy=\bigg((9x)/(3√(x))-(2)/(3√(x))\bigg)dx}`

`{:\implies \quad \sf dy=\bigg(3√(x)-(2(x)^(\footnotesize -\frac12))/(3)\bigg)dx}`

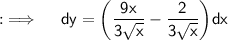
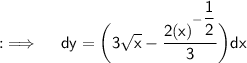
Integrating both sides ;

`{:\implies \quad \displaystyle \sf \int dy=\int \bigg(3√(x)-(2(x)^(\footnotesize -\frac12))/(3)\bigg)dx}`

`{:\implies \quad \displaystyle \sf y=\int 3(x)^(\footnotesize \frac12)\:dx-\int (2(x)^(\footnotesize -\frac12))/(3)\:dx}`

`{:\implies \quad \displaystyle \sf y=3\int (x)^(\footnotesize \frac12)\:dx-\frac23 \int (x)^(\footnotesize -\frac12)\:dx}`

`{:\implies \quad \displaystyle \sf y=3*((x)^(\footnotesize \frac32))/(\frac32)-(2)/(3)* ((x)^(\footnotesize \frac12))/(\frac12)+C}`

`{:\implies \quad \bf \therefore \quad \underline{\underline{y=2x√(x)-(4)/(3)√(x)+C}}}`

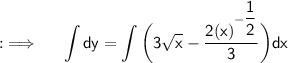
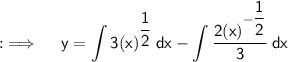
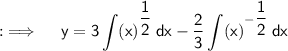
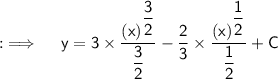
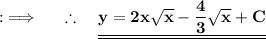
Question 2 :-

Refer to the attachment for this answer

Answer 2

See Below.

Explanation:

Problem #2

We want to find the general expression for the differential equation:

`\displaystyle (dy)/(dx) = (9x-2)/(3√(x))`

Separation of variables:

`\displaystyle dy = (9x-2)/(3√(x)) \, dx`

Take the indefinite integral of both sides and integrate:

`\displaystyle \begin{aligned} \int 1 \, dy & = \int (9x-2)/(3√(x)) \, dx \\ \\ y & = \int (9x)/(3√(x)) - (2)/(3√(x))\,dx \\ \\ & = \int 3 x\cdot x^(-1/2) \, dx +\int -(2)/(3)x^(-1/2)\, dx \\ \\ & = 3\int x^(1/2) \, dx -(2)/(3)\int x^(-1/2) \, dx \\ \\ & = 3\left((2)/(3)x^(3/2)\right)-(2)/(3)\left(2x^(1/2)\right) \\ \\ & = 2x^(3/2) -(4)/(3)√(x) + C\end{aligned}`

Hence, the general expression is:

`\displaystyle y = 2x^(3/2) -(4)/(3)√(x) + C`

Problem #3

We want to evaluate the integral:

`\displaystyle \int \left( 5-x^2 + (18)/(x^4)\right) \, dx`

Apply the power rule for integrals:

`\displaystyle \begin{aligned} \int \left(5-x^2+(18)/(x^4)\right)\, dx & = \int \left(5x^0-x^2+18x^(-4)\right)\, dx \\ \\ & = 5x-(1)/(3)x^3+18\left(-(1)/(3)x^(-3)\right) + C \\ \\ & = 5x-(1)/(3)x^3 -(18)/(3)x^(-3) + C \\ \\ & = 5x-(1)/(3)x^3-(6)/(x^3) + C\end{aligned}`

In conclusion:

`\displaystyle \begin{aligned} \int \left(5-x^2+(18)/(x^4)\right)\, dx & = 5x-(1)/(3)x^3-(6)/(x^3) + C\end{aligned}`