Question

When 4050 joules of heat were applied to 150g of aluminum, the final temperature was 50 degree Celsius. What was the initial temperature? Take specific heat capacity of aluminum as 900J/kg degree Celsius.

Answer 1

`\boxed {\boxed {\sf 20 \textdegree C}}`

Step-by-step explanation:

We are asked to find the initial temperature of aluminum. We will use the following formula.

`q= mc \Delta T`

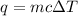
Where q is the heat energy, m is the mass, c is the specific heat capacity, and ΔT is the change in temperature, which is also the difference between the final and initial temperature.

`q= mc (T_f-T_i)`

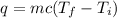
We know the heat energy applied is 4050 Joules, the mass is 150 grams, the final temperature is 50 degrees Celsius and the specific heat is 900 Joules per kilogram degree Celsius.

We must convert the mass to kilograms because the specific heat is in kilograms. 1 kilogram contains 1000 grams.

• 
  `\frac { 1 \ kg }{1000 g }`

• 
  `150 \ g *( 1 \ kg )/(1000 g ) = 150 * \frac {1}{1000} \ kg = 0.150 \ kg`

Substitute all the known values into the formula.

• q= 4050 J
• m= 0.150 kg
• c = 900 J/g °C
• 
  `T_f`= 50°C

`4050 \ J = (0.150 \ kg )(900 \ J/kg \textdegree C)(50 \textdegree C -T_i)`

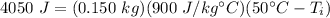
We are solving for the initial temperature, so we must isolate the variable
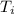`T_i`It is being multiplied by 0.150 kilograms and 900 Joules per kilogram degree Celsius. The inverse operation of multiplication is division, so we divide by both values.

`\frac {4050 \ J}{ (0.150 \ kg )(900 \ J/kg \textdegree C)}= ((0.150 \ kg )(900 \ J/kg \textdegree C)(50 \textdegree C -T_i))/((0.150 \ kg )(900 \ J/kg \textdegree C))`

`\frac {4050 \ J}{ (0.150 \ kg )(900 \ J/kg \textdegree C)}=(50 \textdegree C -T_i)}`

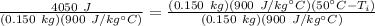
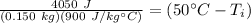
The units of Joules and kilograms cancel.

`\frac {4050 }{ (0.150 )(900 \ \textdegree C)}=(50 \textdegree C -T_i)}`

`\frac {4050}{135} \textdegree C = (50 \textdegree C -T_i)`

`30 \textdegree C = (50 \textdegree C -T_i)`

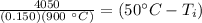
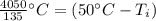
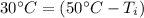
50 degrees Celsius is being added to
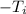`-T_i`. The inverse operation of addition is subtraction. Subtract 50 degrees Celsius from both sides.

`30 \textdegree C - 50 \textdegree C= 50 \textdegree C - 50 \textdegree C - T_i`

`-20 \textdegree C = -Ti`

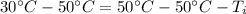
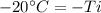
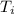`T_i` is being multiplied by -1. The inverse operation of multiplication is division. Divide both sides by -1.

`\frac {-20 \textdegree C}{-1}= (-T_i)/(-1)`

`20 \textdegree C = T_i`

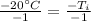
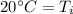
The initial temperature of the aluminum was 20 degrees Celsius.