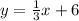Answer:
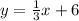
Explanation:

Step 1. Find the slope (by using the slope-formula)
m = slope
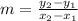
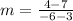
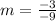
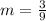
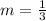
Step 2. Write the equation (using the slope and the points)
Here's how to do it:
Slope-intercept Formula
 whrere m = slope and b = y-intercept
whrere m = slope and b = y-intercept
Plug in the slope into the Slope-intercept Formula
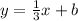
Find the y-intercept (b) by using a point and substituting their x and y values
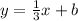
Point: (3, 7)
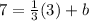

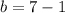
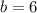
Step 3. Write the equation in Slope-intercept form