Answer:
∠YDC measures 140°.
Explanation:
We can consider using the Exterior Angle Theorem. According to the theorem, the exterior angle of a triangle is equal to the two opposite interior angles.
In other words:
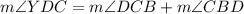
Substitute:
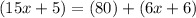
Solve for x. Combine like terms:
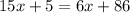
Simplify:
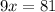
And divide. Hence, the value of x is:
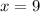
∠YDC is given by:
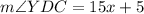
Since we now know the value of x, substitute and evaluate:
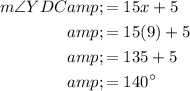
In conclusion, ∠YDC measures 140°.