Question

1. Determine the set of each of the following equations for 0° ≤ x 360° or 0° ≤ t ≤ 360°

a) sin 2 x°= 1/2√2

2. find all the solution in the interval 0° ≤ z ≤ 360° of the following equation
sin 3 z = - 0,42

Please help Me​
SOS

Answer 1

a).

`\sin(2x) = (1)/(2 √(2) ) \\ \\ 2x = { \sin }^( - 1) ( (1)/(2 √(2) ) ) \\ \\ 2x = 45 \degree`

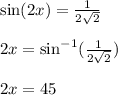
since sine is in the 2nd quadrant, other angle = 180° - x:

`2x = 45 \degree, \: 135 \degree`

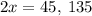
we must make two rotations since it's a double angle:

`2x = 45 \degree, \: 135\degree, \: 225\degree, \: 315\degree, \: 495\degree, \: 675\degree \\`

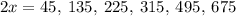
divide each angle by 2:

`x = 22.5\degree, \: 67.5\degree, \: 112.5\degree, \: 157.5\degree, \: 247.5\degree, \: 337.5\degree \\`

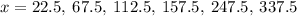
Answer = {x: x = 22.5°, 67.5°, 112.5°, 157.5°, 247.5, 337.5°}

b).

`\sin(3z) = - 0.42 \\ 3z = { \sin }^( - 1) ( - 0.42)`

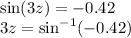
since ans is negative, we take the quadrants of cosine and tangent:

`3z = 204.8\degree, \: 335.2\degree`

we make three rotations:

`3z = 384.8\degree, \: 515.2\degree, \: 695.2\degree, \: 875.2\degree, \: 1055.2\degree, \\`

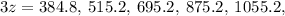
answer is {z : z = 128.3°, 171.7°, 231.7°, 291.7°, 351.7°}