Question

Use Green's Theorem to evaluate the line integral along the given positively oriented curve. ∫C (3y +5e√x)dx + (10x + 3 cos y2)dy C is the boundary of the region enclosed by the parabolas y = x2 and x = y2

Answer 1

By Green's theorem, the line integral

`\displaystyle \int_C f(x,y)\,\mathrm dx + g(x,y)\,\mathrm dy`

is equivalent to the double integral

`\displaystyle \iint_D (\partial g)/(\partial x) - (\partial f)/(\partial y) \,\mathrm dx\,\mathrm dy`

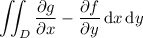
where D is the region bounded by the curve C, provided that this integrand has no singularities anywhere within D or on its boundary.

It's a bit difficult to make out what your integral should say, but I'd hazard a guess of

`\displaystyle \int_C \left(3y+5e^(-x)\right)\,\mathrm dx + \left(10x+3\cos\left(y^2\right)\right)\,\mathrm dy`

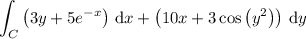
Then the region D is

D = {(x, y) : 0 ≤ x ≤ 1 and x ² ≤ y ≤ √x}

so the line integral is equal to

`\displaystyle \int_0^1\int_(x^2)^(\sqrt x) (\partial\left(10x+3\cos\left(y^2\right)\right))/(\partial x) - (\partial\left(3y+5e^(-x)\right))/(\partial y)\,\mathrm dy\,\mathrm dx \\\\ = \int_0^1 \int_(x^2)^(\sqrt x) (10-3)\,\mathrm dy\,\mathrm dx \\\\ = 7\int_0^1 \int_(x^2)^(\sqrt x) \mathrm dy\,\mathrm dx`

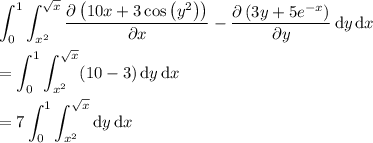
which in this case is 7 times the area of D.

The remaining integral is trivial:

`\displaystyle 7\int_0^1\int_(x^2)^(\sqrt x)\mathrm dy\,\mathrm dx = 7\int_0^1y\bigg|_(y=x^2)^(y=\sqrt x)\,\mathrm dx \\\\ = 7 \int_0^1\left(\sqrt x-x^2\right)\,\mathrm dx \\\\ = 7 \left(\frac23x^(3/2)-\frac13x^3\right)\bigg|_(x=0)^(x=1) = 7\left(\frac23-\frac13\right) = \boxed{\frac73}`