Answer:
Explanation:
You have to solve this as a system. We have 3 coordinates given; the first 2 are given as zeros of the quadratic, the 3rd one is given as a regular coordinate. The zeros of a quadratic are where the y values of a coordinate are 0's because the x-intercepts of a quadratic (aka zeros) exist where y = 0. We use each of those points in the standard form of a quadratic to solve for a, b, and c. First, (0, 0):
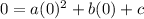which gives us that c = 0. We'll use that value of c as we move forward with the problem. Next we'll use (3, 0):
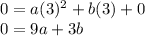Hold that thought for a minute or 2. Next we'll use the coordinate (1, 6):
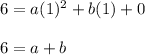Now we have a system that we can solve using either substitution or elimination for a and b. I used elimination:
6 = a + b
0 = 9a + 3b and multiply the top equation by -3:
-18 = -3a - 3b
0 = 9a + 3b
so
-18 = 6a and
a = -3. Now back solve for b:
6 = -3 + b so
b = 9 and our quadratic is
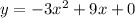or just
