Answer:
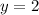
Explanation:
To solve this question, we can use the point-slope formula as we are given points on the line. This is the format:
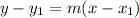
The first step is to find the slope by substituting in two of the points. Let's try using (7,2) and (3,2):

So now we have found that our slope is 0 meaning it is a flat line (shown by the unchanging y values through all three points).
The form for line equations is:
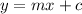
However, since our m=0, it is simplified to this:
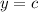
The y-value for all the points is 2, meaning c=2 (as it is also the y-intercept)
Therefore our final equation is:
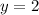
Hope this helped!