Question

2/4.7+2/7.10+2/10.13+2/13.16+.....+2/49.52

tính giá trị biểu thức

Answer 1

It looks like you're trying to evaluate the sum,

`\displaystyle \frac2{4*7} + \frac2{7*10} + \frac2{10*13}+\cdots+\frac2{49*52}`

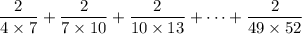
which can be written as

`\displaystyle \sum_(n=1)^(16) \frac2{(3n+1)(3n+4)}`

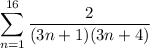
Split up the summand into partial fractions:

`\displaystyle \frac2{(3n+1)(3n+4)} = \frac a{3n+1} + \frac b{3n+4} \\\\ \implies 2 = a(3n+4)+b(3n+1) \\\\ \implies 2 = (3a+3b)n+4a+b`

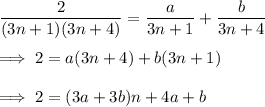
so that

3a + 3b = 0, or a = -b

4a + b = 2

Solve for a and b :

4a + (-a) = 3a = 2 ==> a = 2/3 ==> b = -2/3

So the sum is

`\displaystyle \frac23 \sum_(n=1)^(16) \left(\frac1{3n+1} - \frac1{3n+4}\right)`

Write out the first terms and observe that several terms cancel with each other:

2/3 (1/4 - 1/7)

+ 2/3 (1/7 - 1/10)

+ 2/3 (1/10 - 1/13)

+ …

+ 2/3 (1/43 - 1/46)

+ 2/3 (1/46 - 1/49)

+ 2/3 (1/49 - 1/52)

So the sum collapses and simplifies to

`\displaystyle \sum_(n=1)^(16) \frac2{(3n+1)(3n+4)} = \frac23 \left(\frac14 - \frac1{52}\right) = \boxed{\frac2{13}}`